CRF原理初探

写在前面：本人刚刚入门NLP三个月，希望通过记录博客来巩固自己的知识，增进对知识的理解。

本人在进行序列标注(sequence tagging)方面的学习时，最先接触到两个经典的统计学习方法：一个是HMM(隐马尔可夫模型)，一个是CRF(条件随机场)。在查阅CRF有关的文章时，发现大体分为两类：一类硬核解析，从公式出发；一类重视概念，从原理出发。很多博文都写的很好，不过本人认为，理解CRF，数学与概念都要重视，才能见效。希望这篇肤浅的文章能够帮助像我一样刚入门的NLPer扫去一些疑惑。

一、序列标注 Sequence tagging

了解CRF之前，先从序列标注开始讲起。

序列标注问题是NLP中的基本问题，简单来说就是对一段序列进行标注或者说打标签。许多经典的NLP任务，像词性标注、分词、命名实体识别、拼音输入法等等，本质上都是对句子中的元素进行标签预测。序列标注也是很多更高层次NLP任务的前驱，因为最近做的是分词任务，所以简单说明一下常见的标注方式，便于读者后续阅读：

1. BIO标注：B-Beginning 一个词的开始；I-Inside 一个词之中；O-Outside 独立的字。(常见于命名实体识别，B-Name等等形式)
2. BMES标注：B-Begin 一个词的开始；E-End 一个词的结束；M-Middle 一个词的中间；S-Single 独立的字。（常用于中文分词）
3. BIOES标注：和1、2中字母含义相同。

接下来，一起来看看CRF吧！

二、为什么需要CRF？

先说个人结论：CRF能在训练语料中学习到更多信息，表征出更多特征。

我看过一个很有趣的例子，原文在这儿，翻译在这儿，大概思想就是，你手头有一组图片，图片顺序展示了一个人一天的生活。现在，需要你对这一组图片进行标注，注明这个人在做什么事情，你会怎么去做？

一般来说，我们会一张一张地看，有时候还需要借助前后照片进行推理。因为这组图片是具有时空顺序关系的，上一张图片如果在吃饭下一张图片不可能会在做饭。

CRF的核心思想也是这样，通过对某一时刻与相邻时刻之间的特征进行学习，来获得更好的预测效果。其实如果是之前有了解神经网络的朋友的话，看到这里也一定会想到LSTM模型吧？LSTM模型也很适用于解决序列类型问题，因此，像模型Bi-LSTM会后接CRF层来获得更丰富的标签之间的特征信息。

为了显示CRF在分词时对训练数据更强的学习能力，展示一个例子（拿HMM作比较）：

对于训练数据中出现过的句子(BMES标注)： [为/S 本/S 单/B 位/E 服/B 务/E 的/S 地/B 震/E 监/B 测/E 台/B 网/E]

对应的分词结果应该为： [‘为’, ‘本’, ‘单位’, ‘服务’, ‘的’, ‘地震’, ‘监测’, ‘台网’]

HMM预测结果：

CRF预测结果：

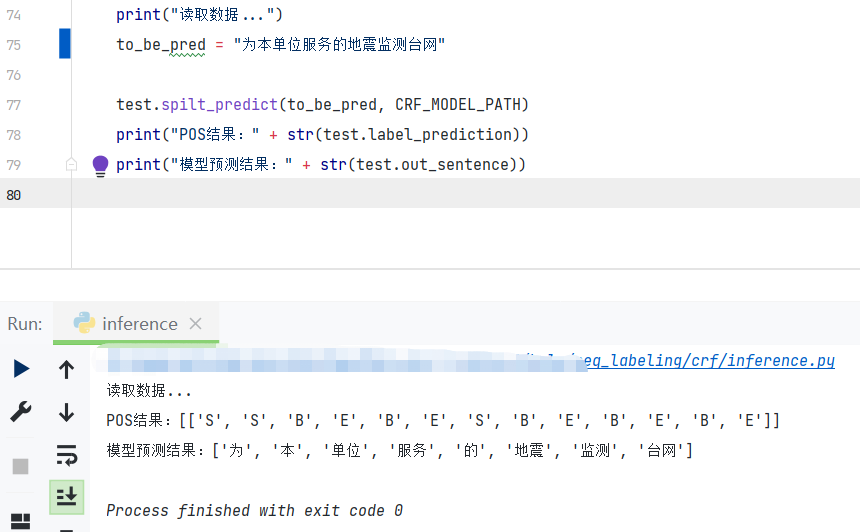
可以看出，CRF在遇到训练数据中出现过的序列，能体现出自身学习到的信息进行标注，对于训练数据提供的潜藏信息的表征能力更强。

接下来，让我们更进一步地了解CRF的性质与不同之处。

三、判别式(Discriminative)模型与生成式(Generative)模型

这两个概念是经常容易碰到的概念，也是我觉得比较基础不能混淆的知识。

先放一张直观的图：

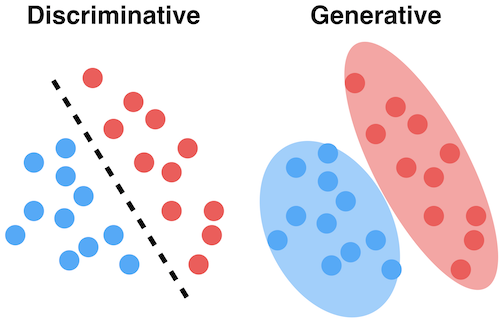
1. 什么是判别式？

   顾名思义，判别式就是，根据xx判断xx。对于输入X，预测标记Y，即条件概率P(Y|X)。所以在我的理解中，判别式其实是在训练中学习得到一个边界条件，或者说分裂面，对于模型的输入，可以直接通过这个判断标准来进行分类。像上图中的左半部分，其实得到的是两个类别的不同点，因此判别式在分类预测任务中有着非常不错的表现。

2. 什么是生成式？

   顾名思义，生成式就是，根据训练数据生成多个种类的“模型”，而不是像判别式一样去学习各个种类之间的分界。因此，这种方式计算的是一种联合概率P(X,Y)，对于输入X，计算多个联合概率，取最大的作为最有可能的情况。像上图中的右图所示，生成式会学习出比较完整的这一整个类的边界，而不是仅仅关注类之间的关系。

3. 举个栗子

   现在我的训练数据里有可口可乐与百事可乐，然后我向训练好的机器输入一张含有易拉罐的图片。

   假如是判别式模型：先对图片提取出特征信息，判别式模型通过一些显著的区分特征(颜色、LOGO等等)，直接可以给出是可口可乐的概率和是百事可乐的概率。

   假如是生成式模型：先对图片提取出特征信息，再通过训练时已经对可口可乐和百事可乐建立好的模型，逐个传入图片特征进行计算，最后概率最高的那个就是预测得到的种类。

4. 和CRF有什么关系？

   HMM是生成式模型，CRF是判别式模型。为什么？因为HMM的训练过程是对所有样本建立一个统计学的概率密度模型，这个模型是通过HMM当中的转移矩阵和发射矩阵实现的。而CRF不同，CRF计算的是条件概率，直接对训练数据中获取的分类规则进行建模，例如前后位置数据与当前位置数据之间的关系等等。CRF更注重的是通过特征函数学习到序列的特征特点，以及序列之中的约束条件。这也就是为什么CRF不会出现第二点中HMM出现的问题，因为HMM只对一个字以及它的下一个字是什么做了概率估计，并没有真正关注到整句话里的前后特征。

   事实上，判别式模型与生成式模型是有一定的转化关系的。逻辑上可以理解为，生成式模型对各个种类建立模型之后，其实也得到了各个模型的边界，提供了转化为判别式的前提条件。对HMM有所了解的读者也可以思考一个问题，HMM与CRF是否存在一定的转化关系？

四、从马尔可夫到CRF

1. 随机场

   在一个样本空间中，各个点的值是根据某种分布随即赋予的。

2. 马尔可夫随机场

   随机场+马尔可夫性，即随机场中某个位置只与其相邻位置的值有关，与不相邻位置的值无关。

3. 条件随机场

   特殊的马尔科夫随机场，Y满足马尔可夫性。随机场中每一个位置下还有一个观测值X(observation)，本质上，就是给定了观测值X的随机场，这个场中有X和Y两种随机变量，且Y满足马尔可夫性。

4. 线性链条件随机场 Linear-CRF

   最常见的CRF的形式，特点是X和Y都具有相同的结构，并且满足马尔可夫性，即随机场中某个位置只与其相邻位置的值有关，与不相邻位置的值无关。

   Linear-CRF示意图：

   

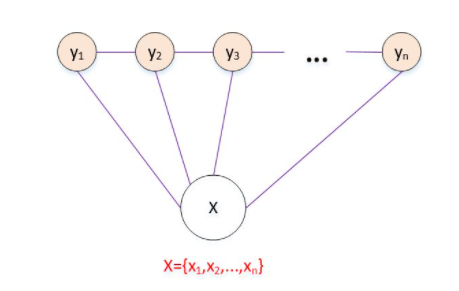
五、最大熵模型与CRF

1. 最大熵 MaxEnt

   最大熵模型不仅仅应用在序列标注任务上，该模型最伟大的地方在于，引入了特征函数以及其相对应的参数来对输入的整体特征进行学习。数学公式就不搬上来了，其实整体上与CRF最后的结果很相似。

   个人理解中，特征函数的引入是为了引导模型去学习我们认为对于任务有帮助的一些特征。 通过这种方式建立起对条件概率的计算，成为了判别式模型。而单纯的生成式模型不含有特征函数，直接对整个数据的分布进行相应的学习。

2. 最大熵马尔可夫模型 MEMM

   MEMM相比于HMM模型进步的地方在于，学习了MaxEnt的方法来计算条件概率。但是它的局限性在于，MEMM是在每个局部节点进行计算的基础上，再合并起来。这样做的问题在于，每一步的最大熵模型得到的条件概率仅基于与这一点相关的两点的信息，并且也只是在这个局部进行归一化，缺乏全局性。

   MEMM的进步之处在于，引入了判别式的方法，又基于HMM的性质在局部进行运算，速度也很快。

3. CRF中的特征函数

   CRF更像是以上几种方法的结晶。

   CRF中不可或缺的概念就是特征函数。一开始在我看CRF的时候，突然蹦出两个特征函数搞得我一头雾水，后来我才发现原来都是在前人不断地研究和试错中慢慢摸索出来的模型，respect。特征函数其实是人为定义的，比如在分词任务中，我不希望动词后面会加形容词或者动词，那么我可以通过设置特征函数来明确这一点，给机器一个调整的方向。

   CRF的特征函数有两种：

   ① 节点上的状态特征函数：
   $
   s_l(y_i,x,i),i=1,2,…,L
   $

   表示出节点上观察序列与对应状态之间的特征。

   ② 节点之间的转移特征函数：
   $
   t_k(y_{i-1},y_i,x,i),k=1,2,…,K
   $

   表现出节点之间(这里是前一个节点与当前节点)的特征关系。

六、CRF公式浅析

进入公式环节，在此之前，还要先补充一点方便理解的知识：

1. 概率无向图

   实际上，如果联合概率分布满足成对，局部或全局马尔可夫性，就称此联合概率分布为概率无向图模型。这个定义和上面马尔可夫场的定义是相似的。也就是说，可以把马尔科夫场看作一个概率无向图，点是随机变量，边是变量间关系。而条件随机场又可以看作是特殊的马尔科夫随机场，故而可以用概率无向图来进行表示。

   在概率无向图中，还有一个很重要的概念，叫做最大团。

   

   感谢这篇文章，这组图片说明的很清楚。其实很简单，极大团中是全连接的一组节点，再多一个节点就会破坏这种全连接的条件限制。最大团就是极大团中节点数最多的极大团。

   那我们为什么需要最大团呢？因为根据一个很数学的定理(Hammersley-Clifford 定理)，概率无向图模型的联合概率分布P(Y)可由最大团得到：

   $
   P(Y) = \frac{1}{Z}\sum_{Y}\psi_c(Y_c)
   $

   $
   Z = \sum_Y \prod_c\psi_c(Y_c)
   $

   $
   \psi_c(Y_c) = e^{-E(Y_c)}
   $

   $
   E(x_c) = \sum_{u,v\in C,u \neq v}\alpha_{u,v}t_{u,v}(u,v) + \sum_{v \in C}\beta_v s_v(v)
   $

   第一条公式里的c，就是无向图的最大团。${Y_c}$代表了节点上的随机变量，${\psi_c}$是一个严格正函数，Z是归一化因子。

   第二条公式是归一化因子的计算公式。与第一条公式相同，只不过增加了对所有最大团的连乘。

   第三和第四条公式是对${\psi}$函数，或者说，势函数的进一步解释。但实际上，并没有规定${\psi}$函数一定是这样。
   因为这里的定义与物理中的玻尔兹曼分布有关，所以一般这样设置势函数。这里的${\alpha}$与${\beta}$都是参数，t()与s()是特征函数。
   还有一个细节，这里的特征函数t()是关于极大团中两个节点之间的关系，而s()是关于节点单独的。这与CRF中特征函数的定义很相似。

   公式没有看得很明白也没有关系，读者是否发现，第四条公式非常的眼熟？让我们继续来观察一下CRF的公式。

2. CRF公式

   为了便于说明，以线性条件随机场为例。

   CRF的参数化定义是这样的：
   $
   P(y|x) = \frac{1}{Z(x)}exp(\sum_{i,k}\lambda_kt_k(y_{i-1},y_i,x,i) + \sum_{i,l}\mu_ls_l(y_i,x,i))
   $

   $
   Z(x) = \sum_y exp(\sum_{i,k}\lambda_kt_k(y_{i-1},y_i,x,i) + \sum_{i,l}\mu_ls_l(y_i,x,i))
   $

   是不是很眼熟？其实就是把概率无向图中的公式整合了一下嘛！λ和μ都是可学习的参数，特征函数也和我们前面定义的一样。其实，MEMM最大熵的计算公式也和这个结果非常相似，因为信息熵的定义和设计本身就与这里的势函数有一些相似之处。但是它与CRF不同的地方主要在于，归一化因子的计算不同。MEMM计算的归一化因子是各个节点上归一化因子连乘得到(个人观察，不一定正确)；CRF直接计算全局的归一化因子，因此全局性更强。

   看到这里，是不是大概明白CRF的公式来源于哪里了？

   为了表达方便，一般会对公式进行简化如下：

   $
   P(y|x) = \frac{1}{Z(x)}exp(\sum_{k}\omega_kf_k(y,x))
   $

   $
   Z(x) = \sum_Y exp(\sum_{k}\omega_kf_k(y,x))
   $

   用ω来代替表示两个参数，用 f() 来代替表示两个特征函数。用了这个公式之后，其实我们能发现CRF的一些工作原理。满足特征函数数量越多，相应的条件概率值就会越大(不将ω考虑进来，将ω考虑进来的话应该加一个前提：在我们希望学习的特征情况下。)

   至此，就可以通过一些算法(梯度下降、L-BFGS等等)进行学习，得到参数了。

七、总结

个人认为，CRF最核心的点莫过于引入全局性。上面的例子讲的是Linear-CRF的情况，实际上，CRF可以复杂得多，这一切都由你的特征函数来确定。CRF的这种设计方式使得它能挖掘出更多的标签之间的约束关系和信息，但是缺点也比较明显，就是训练速度会比较慢。
最后，感谢俊毅哥还有KNLP组中其他的小伙伴们！！